La formation continue des enseignants : phénomène naturel ?

Eric Barbazo (Président de l’APMEP, I.R.E.M. d’Aquitaine)

Introduction

La formation continue des enseignants nous apparaît en ce début du 21ème siècle, comme allant de soi et indispensable à l’adaptation des pratiques et des contenus d’enseignement qui n’ont de cesse d’évoluer. Pourtant, si on considère la période de l’enseignement secondaire depuis la création des lycées sous l’Empire de Napoléon, la formation continue constitue un phénomène très récent qui débute seulement à la fin des années 1960.

Ainsi, la question qui va nous intéresser devient alors : la formation continue est elle un phénomène si naturel que cela, au sens où, pendant près de cent cinquante ans, les professeurs titulaires, et notamment ceux qui sont recrutés par le concours de l’agrégation, ont une carrière basée sur leur seule formation disciplinaire initiale et ne manifestent pas le besoin de réactualiser leur connaissances.

Il s’agit donc ici, de montrer les étapes du processus qui a conduit à l’émergence d’un besoin de formation pendant la carrière. Nous nous appuierons en particulier sur trois facteurs dont la concordance paraît nécessaire à cette émergence, à savoir :

• les réformes structurelles de l’enseignement secondaire, c’est à dire d’une part, les réformes des différents cycles, des séries et niveaux d’enseignement qui décident de la place et donc de l’importance de telle ou telle discipline dans le cursus de l’élève, phénomène particulièrement vrai en mathématiques et d’autre part, des différents ordres d’enseignement qui déterminent les statuts des professeurs ;
• les réformes des contenus disciplinaires ;
• la prise de conscience de la nécessité d’introduire une dimension pédagogique au métier de professeur qui doit en particulier s’apprendre en même temps que la discipline.

Ces trois facteurs sont déterminants car nous allons voir que si, dans toute la première moitié du 20ème siècle, on peut distinguer, à l’état embryonnaire, ce que l’on aimerait appeler formation continue, visible notamment dans les activités des associations de spécialistes, c’est bien la conjonction de ces trois facteurs qui conduit, à partir des années 1950, à faire apparaître tout d’abord la nécessité d’une information des enseignants, traduite ensuite en terme de formation continue.

Nous allons ainsi traiter cette problématique en trois parties, considérant d’abord la période embryonnaire entre 1902 et 1945. En second lieu, nous verrons quelle forme prend l’information des enseignants au lendemain de la Seconde guerre mondiale. Nous terminerons enfin par les étapes qui ont conduit à la création des I.R.E.M., véritables outils et symboles d’une formation continue en marche.

I. L’état embryonnaire

Il est nécessaire de faire un parcours depuis 1902 pour montrer pourquoi la formation continue n’apparaît pas si facilement. La réforme de 1902 est une réforme structurelle très importante pour tout l’enseignement secondaire et pour l’enseignement des sciences et des mathématiques en particulier. Rappelons rapidement sa principale innovation : il s’agit de la création de séries à partir de la classe de sixième :

Deux séries de la sixième à la troisième, A et B, qui diffèrent par le latin et le grec et les horaires en sciences (2 heures en 6e A et trois heures en B mais la série A est plus théorique et moins appliquée).

Quatre séries à partir de la seconde : A, B, C et D. Deux séries terminales, Philo et Mathématiques avec options également A et B.

C’est donc une nouveauté très importante par rapport à l’enseignement secondaire du 19ème siècle car les séries et notamment la série C à partir de la seconde (mathématiques latin) attire très rapidement les meilleurs élèves. Nous n’allons pas revenir sur les raisons de cette réforme, cela a déjà été fait en détail par Hélène Gispert [1] et Nicole Hulin [2]. Rappelons seulement quelques grandes lignes : son origine est universitaire, elle hisse l’enseignement de la science au niveau de l’enseignement classique latin grec, elle instaure une réelle formation scientifique. Sur le plan des contenus, peu de modifications sont à relever, si ce n’est l’introduction du calcul différentiel en seconde et intégral en terminale.

En revanche, l’histoire de l’A.P.M.E.P. nous apprend que cette réforme a profondément modifié les pratiques des professeurs de mathématiques. En effet, l’enseignement des mathématiques devient pyramidal, c’est à dire qu’une notion apprise au niveau n est utilisée au niveau n+1. C’est la première fois, car jusqu’à la fin du 19ème siècle, la formation en mathématiques ne se faisait réellement qu’en classe de mathématiques, c’est à dire dans l’année de préparation du baccalauréat sciences, et ce qui avait été vu auparavant ne relevait que de culture scientifique. On peut également ajouter qu’au 19ème siècle, le baccalauréat sciences ne se passait qu’après obtention du baccalauréat philo. Cette caractéristique pyramidale et ses conséquences sont clairement décrites dans les bulletins de l’A.P.M.E.P. [3]. Avec la réforme de 1902, les connaissances des élèves se suivent depuis la 6ème et surtout, entre la seconde C et la classe de mathématiques. Les professeurs se confrontent donc à ce qu’ont fait leurs collègues les années précédentes, comme le montre le rapport de M. Huard pour l’assemblée générale de 1913 :

Il ne faut pas oublier, en effet, que, depuis la réforme de 1902, les conditions d’enseignement ont changé. Auparavant, la formation mathématique des élèves se faisait surtout en classe d’Elémentaires. Devant des élèves ayant plus ou moins de connaissances mathématiques antérieures, mais d’un âge déjà avancé et par suite d’une certaine maturité, le professeur reprenait tout le cours depuis le commencement : ce professeur unique pouvait employer les notations et les définitions qui lui semblaient les meilleures ; lui seul formait les élèves et son enseignement constituait un tout cohérent et homogène. Peu importait que ce qu’il faisait différât dans la forme de ce qui se faisait à côté.

Ceci est très nouveau pour un grand nombre de professeurs et pose un problème qu’il est nécessaire de résoudre : celui de l’harmonisation des notations mathématiques et des définitions employées puisque dans cet enseignement pyramidal, un suivi pédagogique s’impose dorénavant. C’est à partir du rapport de M. Huard que l’association pose la question de cette unification. L’idée est de faire des propositions de termes ou de notations, soit pour palier à un manque, soit pour pouvoir parler de la même manière de la même chose. Ces propositions sont relayées par le bulletin de l’association jusqu’à ce qu’un consensus se fasse. Puis, s’il y a consensus, il est décidé de faire voter en assemblée générale un accord autour de ces définitions et notations et une recommandation à les utiliser. Durant l’entre deux guerres, les notations et définitions suivantes sont adoptées :

• Quotient entier, quotient exact, valeur absolue, centre d’homothétie (assemblée générale de 1922) ;
• Droite, segment, direction, orientation, droite orientée ou axe, vecteur (comme segment orienté), origine, extrémité d’un vecteur, support d’un vecteur, notation du vecteur avec la flèche (assemblée générale de 1923)
• Nombre algébrique : nombre positif, nul ou négatif (assemblée générale de 1924) ;
• Angle 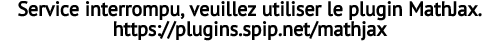 [4], médiatrice d’une segment, médiatrice d’un triangle, plan médiateur d’un segment, plan frontal de projection (assemblée générale de 1925) ;
• Produit scalaire par la notation 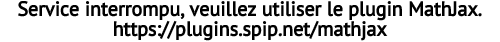, produit vectoriel noté 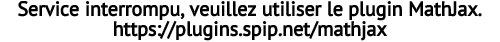(assemblée générale de 1929)
• Moment d’un couple au lieu d’axe d’un couple ; homothétie positive, homothétie négative (ne pas employer le terme antihomologue) (assemblée générale de 1933)
• Bande (portion de plan entre deux droites parallèles), radicande, inéquation à la place de « inégalité conditionnelle », (assemblée générale de 1939)
• Perpendiculaires (droites coplanaires dont l’angle est droit), droites orthogonales (droites quelconques dont l’angle est droit) (assemblée générale de 1947 [5])

Cette unification n’est pas toujours bien vue. Il y a les « contre », c’est à dire ceux qui défendent la liberté pédagogique du professeur avant tout et ne veulent donc rien sembler imposer, les radicaux qui veulent construire un vocabulaire complètement nouveau et adapter même l’existant, comme par exemple remplacer triangle par trigone, au même titre que tétragone, polygones. Puis il y a les modérés qui ne veulent pas chambouler toutes les notations et seulement en créer là où il y a un manque, comme par exemple la médiatrice ou le symbole pour noter le discriminant.

Ce travail est prolongé jusque bien après la seconde guerre mondiale. Il est donc question de donner certaines habitudes aux professeurs en poste, la plupart agrégés, qui ne considèrent pas nécessairement qu’ils aient besoin de formation après le concours durant leur carrière. D’ailleurs, si la réforme de 1902 est structurellement importante, elle reste cantonnée à l’ordre secondaire, c’est à dire à l’enseignement dispensé dans les lycées, enseignement payant et réservé à une élite sociale, qui regroupe une très faible minorité d’élèves. La grande majorité des élèves suit plutôt sa scolarité dans les rangs de l’ordre primaire, les écoles communales, les écoles primaires supérieures et cours complémentaires. Ainsi, il n’y a pas mélange des statuts et les modifications imposées par la réforme de 1902, que ce soit sur le plan de l’adaptation pédagogique dont il a été question ou des contenus qui ne changent pas fondamentalement jusqu’en 1950, restent facilement assimilables par la plupart des agrégés.

On peut en revanche dire que le bulletin de l’association joue en quelque sorte, un rôle d’information pour des changements de pratiques ou de contenus. C’est encore plus prégnant chez les physiciens par exemple, pour qui la réforme de 1902 a eu un impact bien plus important en terme de changement des pratiques d’enseignement puisqu’elle crée des travaux pratiques pour lesquels les professeurs n’ont aucune expérience. Le bulletin de l’Union des physiciens devient alors, dès sa création en 1907, un relais de ce qu’on peut appeler une véritable formation continue, avec une rubrique intitulée le service des renseignements, qui donne des activités clé en main et incite les enseignants à échanger leurs idées et pratiques [6].

Si l’on ne peut parler réellement de formation continue pour les mathématiques durant l’entre deux guerres, et malgré les exemples donnés, on peut distinguer tout de même une certaine prise de conscience générale que le métier évolue et qu’il faut anticiper des changements auxquels contribuent les associations de spécialistes. L’après seconde guerre mondiale voit cette évolution s’accélérer et s’orienter vers une plus large information des enseignants.

II. L’information des enseignants

La paysage éducatif d’après 1945 est bien différent de celui d’avant guerre. Tout d’abord, sur le plan structurel, les écoles primaires supérieures ont disparu depuis 1941. Il reste les lycées avec leur structure inchangée et de l’autre côté, les écoles primaires et les cours complémentaires auquel succèdent dans les années 1950 les collèges d’enseignement général pour l’enseignement court et les Collèges d’enseignement technique, puis en 1963, les Collèges d’enseignement secondaire. Il y a donc une volonté de créer entre le primaire et le secondaire, un cycle d’observation qui est à cheval sur les deux ordres d’enseignement, entre primaire et secondaire et donc avec des enseignants issus de ces deux ordres. Ainsi, de nombreux professeurs du type primaire, anciens instituteurs, professeurs de C.E.G., sont amenés à enseigner en 6e et 5e puis plus tard jusqu’en 3e.

Ce mélange des ordres d’enseignants est bienvenue pour l’association. On le voit très bien dans les bulletins de l’A.P.M.E.P., notamment chez Gilbert Walusisnki qui prône régulièrement l’ouverture de l’association vers un plus grands nombre de professeurs de type primaire et C.E.G.. Pour l’association, c’est une opportunité d’étendre sa représentativité et de multiplier ses adhérents et elle commence dans les années 1960 à s’intéresser aux programmes du primaire et à la formation des professeurs du primaire et secondaire. Mais ce n’est pas sans poser de nombreux problèmes quand il s’agit d’enseigner des mathématiques qui, de plus, deviennent modernes, dès les années 1950 et dès les classes d’initiation.

En effet, depuis la Libération, l’enseignement des mathématiques cherche une voie de modernisation. Cela commence par une réflexion sur une orientation possible de l’enseignement en utilisant la méthode axiomatique. La méthode est réfléchie avant tout comme un outil pédagogique [7]. Elle est présentée comme une méthode d’apprentissage, à partir de termes primitifs et de propriétés initiales, à partir du plus jeune âge. Pour accompagner cette réflexion, une commission intitulée Commission Axiomatique et Redécouverte est créée dans le milieu des années 1950 par l’A.P.M.E.P.. Le terme « axiomatique » figurant dans le nom de la commission est expliqué par son responsable, Yves Crozes, comme affirmant ce qu’il appelle « la droiture du fondamental », c’est à dire l’accès à la logique déductive. Le second terme « redécouverte » écrit-il, « rappelle que notre aventure doit se vivre avec des enfants et pour eux ». C’est donc une position très imprégnée de l’expérience des classes nouvelles de la Libération et des méthodes actives qui faisaient participer l’enfant aux découvertes de son apprentissage.

Cette commission de l’A.P.M.E.P. organise, avec la Société mathématique de France, un cycle de conférences entre 1955 et 1963 qui font intervenir de nombreux universitaires sur les mathématiques modernes. On peut en citer quelques uns : Lichnérowicz, Revuz, Choquet, Dieudonné, Dixmier, Cartan. Les plus fréquents intervenants sont Gustave Choquet et André Revuz. Entre temps, Revuz devient président de l’A.P.M.E.P. de 1960 à 1962. Il rédige à partir de ses conférences, un cours qui s’appelle le cours de l’A.P.M., constitué de trois tomes : groupes anneaux et corps, Espaces vectoriels, Eléments de topologie, publiés par l’association sous la forme de brochures qui se vendent en best-sellers.

On peut affirmer que ces conférences participent de l’acculturation des professeurs de l’enseignement secondaire pour les mathématiques modernes. Toutefois, on ne parle toujours pas de formation continue mais d’information des enseignants. Il faut ajouter à cela que le problème majeur des années 1950-1960, au sein de l’A.P.M.E.P., mais d’une manière plus nationale et également internationale, n’est pas celui de la formation au cours de la carrière, mais plutôt celui de la formation initiale. La pénurie en enseignants est en effet très forte depuis la fin des années 1950 et donne lieu à de nombreux colloques nationaux et internationaux sur ce thème.

Ce qui est remarquable, c’est de voir comment la réflexion sur la formation initiale débouche à terme sur une demande de formation continue. En effet, il est de plus en plus question, depuis le début de la réflexion sur l’utilisation de l’axiomatique qui s’est présentée comme action pédagogique dès les premières classes d’initiation aux mathématiques, d’introduire une dimension pédagogique à la formation initiale des enseignants, y compris dans leur préparation aux concours. En 1960, une grande conférence sur la formation des maîtres est organisée par l’A.P.M.E.P.. Il est préconisé, notamment pour pourvoir enseigner dans le cycle d’orientation et le premier cycle du collège d’enseignement général, d’obtenir le niveau de connaissances correspondant au premier cycle de l’enseignement supérieur, c’est à dire la propédeutique et avoir suivi une année de formation pédagogique. Pour le premier cycle des lycées, le rapport préconise en revanche un certificat d’aptitude comprenant une partie théorique et une partie pratique, à la suite de la formation pédagogique. Pour l’enseignement dans le second cycle, le C.A.P.E.S. reste valable avec une année de formation pédagogique également. Cette demande de formation pédagogique revient donc régulièrement dans toutes les manifestations et commissions organisées par l’A.P.M.E.P. dans les années 1960 et se trouve particulièrement soutenue par Gilbert Walusinski et André Revuz. Il est donc question de modifier assez profondément le recrutement. Par suite, la question du perfectionnement des professeurs en exercice se pose puisqu’ils n’ont, quant à eux, reçu aucune formation au contenu pédagogique. Le rapport que fait l’A.P.M.E.P. sur ce point précise [8] :

On peut citer plusieurs modes possibles de perfectionnement :

III° Stage de plus longue durée

On voit donc qu’en terme de perfectionnement, l’A.P.M. fait référence à ce qui se fait depuis plusieurs années. On peut dorénavant parler d’une revendication de formation continue qui s’accélère à partir de 1963 avec la réforme Fouchet et la création des C.E.S. dans lesquels les professeurs de types primaire et secondaire vont devoir coexister dans leur enseignement en premier cycle. C’est d’ailleurs à cette époque que le terme recyclage apparaît dans les bulletins de l’A.P.M.E.P.. Dès 1964, à Bordeaux par exemple, il y a du recyclage organisé par la régionale de l’association. Ainsi, la conjonction des réformes structurelles, des contenus mathématiques et de la nécessité de prendre en compte la pédagogie comme thème d’étude permet une demande explicite de formation continue. Le terme formation continue est conseillé en 1966 dans le bulletin de l’A.P.M.E.P. : « Nous recommandons l’emploi du terme formation continue plutôt que celle de recyclage ».

Il manque dorénavant un outil de formation continue et ce sera le rôle dévolu aux I.R.E.M..

III. La création des I.R.E.M.

Lors du séminaire A.D.I.R.E.M. de juin 2002, André Revuz affirmait : «  les I.R.E.M. ont une mère, l’A.P.M.E.P., et un père, Gilbert Walusinski  ». Le rôle de Walusinski dans la création des I.R.E.M. est indéniable puisque Gilbert Walusinski consacre de très nombreux articles à ce sujet dans le bulletin de l’A.P.M.E.P.. Toutefois, la création des IREM est due à une convergence d’actions, à la fois personnelles et collectives, que les évènements de 1968 ont précipité. Le propos d’aujourd’hui n’est pas de décerner les médailles individuelles. Il se limite ici à la présentation du rôle de trois personnalités, Gilbert Walusinski, André Revuz et Maurice Glaymann, qui ont eu tour à tour, des responsabilités à l’A.P.M.E.P..

L’idée d’instituts mettant en commun le travail de professeurs des enseignements secondaire et universitaire, caractéristique fondamentale des I.R.E.M., est indéniablement une idée de Gilbert Walusinski. Depuis la fin des années 1950. Elle n’apparaît pas sous ce nom, mais dans la commission qu’il lance sous sa présidence [9] pour traiter de la question de la formation initiale des professeurs, il propose déjà des Instituts de formations de ce type :

Au siège de chaque Académie, et sous l’autorité du Recteur, il est créé un Institut de formation et de recherche pédagogique (I.F.R.P.).
[…]
Remarques sur les I.F.R.P : leur existence au siège de chaque académie peut favoriser :
le développement de la recherche pédagogique théorique et pratique (domaine où les études paraissent moins poussées en France que dans d’autres pays ;
les liaisons utiles entre maîtres des divers ordres d’enseignement en les amenant à coopérer pour la formation des maîtres ; ce faisant, les I.F.R.P. peuvent aider à fonder l’Ecole unique.

On est en 1958. On voit bien que l’idée de départ est double : d’une part, il y a la volonté de fonder une recherche en pédagogie, ce qui constitue une nouveauté fondamentale à la fin des années 1950. D’autre part, la liaison entre les professeurs des différents ordres constitue également le second pilier de cette volonté.

En 1964, Sous l’impulsion de Walusinski toujours, une commission appelée Grande Commission de l’A.P.M.E.P. est créée pour proposer des solutions en terme de formation également. Mais il y a accélération des intentions. La formation des maîtres devient en effet un chapitre du travail de la commission qui doit prendre en charge l’ensemble de la réflexion sur les réformes à entreprendre, réformes générales concernant l’enseignement, allant de la confection des programmes aux méthodes pédagogiques et aux expérimentations à mener. Il est notamment question de la création d’Ecoles d’application où les recherches pédagogiques sont à développer. A la même époque à Bordeaux, Guy Brousseau crée un Centre de Recherche sur l’enseignement des mathématiques (C.R.E.M.) au sein du Centre de recherche et de documentation pédagogique (C.R.D.P.) de Bordeaux.

La Grande Commission de l’A.P.M. prend en 1966 le nom de Commission recherche et réforme qui, peut-on dire, peut être considérée comme l’antichambre de la commission ministérielle présidée par Lichnérowicz, elle même créée en janvier 1967, soit six mois après. Le terme antichambre n’est peut être pas trop fort, si on le mesure, lors de la création de la commission Recherche et réforme, au compte rendu explicite du comité de l’association [10] :

La « Grande Commission » qui prend le nom de « Commission Recherche et Réforme » aura pour but, d’animer, de suivre attentivement les travaux de la Commission ministérielle dont l’A.P.M. demande la création, ou dans le cas où cette création n’interviendrait pas, de la suppléer.

Il faut préciser que le président en exercice est Maurice Glaymann qui sera membre de la commission Lichnérowicz et qui écrit une partie du rapport préliminaire de celle-ci concernant notamment le premier cycle du second degré en liaison avec les expérimentations qui se déroulent dans l’académie de Lyon dès 1964.

Un autre membre influent de la commission Lichnérowicz est André Revuz. Influent, car le travail sur les principes d’une réforme de la formation des professeurs depuis la fin des années 1950 est largement préparé par lui, ainsi que Gilbert Walusinski. Ces actions prennent forme dans les nombreux rapports qui en sont fait dans les bulletins de l’association.

L’ensemble des actions de ces personnages, dont deux sont universitaires et présidents de l’A.P.M.E.P. dans les années qui précèdent immédiatement la création des I.R.E.M., fait que le rapport de la Commission Lichnérowicz entérine les idées de l’A.P.M.E.P. sur les I.R.E.M.. Lorsqu’on compare les rapports de la Commission Recherche et Réforme de l’association et celui de la Commission Lichnérowicz sur les I.R.E.M., ils sont semblables en presque tous les points.

Les ministres Fouchet [11] puis Peyrefitte [12] sont intéressés par le projet d’après ce qu’en disent les rapports des bureaux de l’A.P.M.E.P.. Mais rien ne se passe avant mai 1968 et c’est Edgar Faure qui décide de leur création. Dans le discours d’Edgar Faure qu’il fait à l’assemblée nationale en octobre 1968, une référence au bulletin de l’association montre l’importance qu’il accorde à la transformation de l’enseignement des mathématiques qu’il juge inéluctable [13].

Je lisais le même jour en feuilletant une revue spécialisée : au temps de la machine à vapeur, il suffisait que certains ingénieurs seuls, sachent la théorie de l’intégration. A l’époque des ordinateurs et de l’automatisation, la lecture d’un organigramme et le maniement des symboles doivent faire partie de la culture de tous.

Les trois premiers I.R.E.M. sont créés dès la rentrée 1968 à Paris, Lyon et Strasbourg. Le fait remarquable réside dans le fait que les I.R.E.M. n’ont pas de statut officiel lorsqu’ils commencent à fonctionner. Ils n’existent pas. Ils faut attendre 1970 pour qu’une lettre ministérielle précise leurs missions, qui étaient toutefois indiquées dans le rapport de la commission Lichnérowicz :

Contribution à la formation initiale ; formation continue des enseignants ; contribution à l’expérimentation pédagogique ; élaboration d’une documentation et diffusion.

Les moyens sont immédiatement très importants. Pour l’I.R.E.M. de Paris, les agrégibles c’est à dire les agrégatifs qui n’ont pas voulu passer l’oral et qui attendent, dans un poste, l’année suivante pour repasser le concours, sont employés à L’I.R.E.M. avec trois heures de décharge chacun. Plus de mille séances d’information mathématiques auprès de quelques 1500 maîtres, 6 maîtres assistants à mi temps. 4 bureaux et 3 salles sont alloués pour 15 personnes par salles.

A Lyon, des décharges pour une quinzaine de formateurs, professeurs du secondaire et assistants ou maîtres assistants (quatre en fait) de l’université en demi service. Des centaines d’heures supplémentaires pour que les professeurs viennent se former ainsi que la mise à disposition de 3 bureaux pour 15 personnes par salle.

Du personnel administratif est également attribué aux I.R.E.M. : un psychologue spécialisé ; 1 secrétaire administrative ; 2 dacitlos et 1 agent pour les tirages mis à disposition dans chaque I.R.E.M..
Les professeurs en stage bénéficient de trois heures de décharge pour suivre la formation. En février 1972, alors que 13 I.R.E.M. sont créés, une note du ministère indique un premier bilan :

Crédits de fonctionnements en 1971 pour les I.R.E.M. créés : 3 400 000 Fr portés en 1972 à 4 600 000 Fr.

Crédits en heures supplémentaires : 6 000 000 Fr pour l’année scolaire.

On le voit, les moyens mis à disposition sont effectivement considérables.

Les premiers problèmes ne tardent pas à surgir. Dès la première année, la question se pose de savoir si les I.R.E.M. vont continuer d’être créés. Pourtant, et après rencontres entre l’association et les membres de la Commission Lichénrowicz et du ministère, c’est ce qui se passe au rythme de trois ou quatre par an.

Les ennuis commencent réellement à partir de 1975 car la charge budgétaire est très lourde. En 1978, une pétition est lancée contre l’offensive ministérielle qui met en péril la survie des I.R.E.M.. Notamment soutenue et relayée par la présidente de l’A.P.M.E.P., Christiane Zehren, elle recueille près de 40000 signatures. Dès lors, les crédits ne cessent toutefois de baisser.

Conclusion

On peut dire en premier lieu, que la création des IREM est l’aboutissement d’un processus qui, initialement, prend forme sur la problématique de la formation des professeurs dans son ensemble, formation initiale d’abord puis, plus tard, continue. L’émergence d’une dimension de recherche pédagogique s’impose également dans les débats. Le recyclage, à l’œuvre dès le début des années 1960, n’est qu’une conséquence qui vient du fait qu’il faut bien former aux mathématiques modernes les professeurs qui, pour beaucoup, dans les années 1960 puis 1970, ne les connaissent pas, surtout chez les professeurs de type primaire et C.E.G..

En second lieu, on peut constater que la formation continue constitue finalement un phénomène nouveau dans l’histoire de l’enseignement, si on la place sur l’échelle du développement de l’enseignement secondaire depuis la création du lycée au début du 19e siècle.

Enfin, il y a, de nos jours, incontestablement un essoufflement de cette formation continue, dont l’impact baisse d’années en années. Il reste donc à inventer une dynamique nouvelle, pour une formation continue plus efficace, qui amène alors à poser plusieurs questions :

Faut-il la rendre obligatoire ou la laisser basée sur le volontariat ?

Les IREM existent et il faut faire en sorte de les conserver. Il faut sûrement les faire évoluer peut être en ouvrant leur accès à d’autres disciplines (physique, svt, …)
Peut on trouver des moyens de rendre la formation continue plus valorisante : rémunération en terme d’indice, de développement de carrière, de facilité à mutation, formation diplomante reconnue par l’université, permettant une réorientation, etc.

Plusieurs questions auxquelles il faudra que l’on trouve des réponses collectives et qui pourraient permettre d’anticiper, en liaison avec la formation initiale qui est en train d’être repensée, une réforme de la formation continue des professeurs de l’enseignement secondaire pour les années à venir.