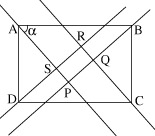
Le problème de Vacquant consiste à mener par les sommets d’un parallélogramme quatre droites deux à deux parallèles. On cherche alors à quelle condition le quadrilatère ainsi formé est un carré.
On donne d’abord une résolution analytique, puis une représentation algébrique du problème permet de traiter plusieurs généralisations. Inutile de partir d’un parallélogramme, un quadrilatère, puis un hexagone font l’affaire.
On termine enfin par des applications possibles dans les classes de Lycée.



Commentaires